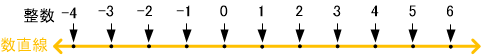
各自15cm程度の長さが図れる物差しを用意してください。
実験に使います。
実験の中では測定値などの数を扱うことが増えてきます。何気なく使っていると数のことをよく知っているつもりになってしまいますが、実は理解できていないことも在るかもしれません。少し復習に付き合ってください。
数えるための数です。リンゴ1個、みかん3個のように使う数です。みかん3個といっても個々のみかんの大きさや状態は違いますが、それを無視して3個です。
順番を表すのにもつかわれます。1番目、2番目、、、、
自然数は 1,2,3,4,5、、、と1つ増やすと次の数になります。下限は1ですが上限はありません。
※ここでは0は含まないことにしています
● 順番に並べることができるので、大きいとか小さいとかの比較が可能です。
● 自然数の間の足し算結果は常に自然数なので、自然数の集合は足し算については閉じています。
掛け算についても同様です。
アラビア数字: 0,
1,2,3,4,5,6,7,8,9,10,11,12、、、、100、、、 (10進数)
※0を自然数に含める扱いもあるので、自然数というときは0を含むか否かを明確にするべき
漢数字: 一、二、三、四、五、六、七、八、九、十、十一、十二、、、、百、、、
ローマ数字: I、II、III、IV、V、VI、VII、VIII、IX、X、XI、VII、、、、C、、、
数字が使われていて、数のように見えても、数でないものが色々あります。
※逆に、数字0〜9以外にアルファベットのA〜Fを使う16進数は、数に見えなくとも数です。
例:学籍番号、電話番号、郵便番号、マイナンバー
名前として数字列を割り当てた例です。国によっては数字だけでなくアルファベットなどの文字を含めて識別用の文字列とすることも在ります。これらの番号は元は番号だったかもしれませんが、自然数とは違って途中の番号が抜けていたりするかもしれません。
※学籍番号は数ではありません、識別用の数字で書かれた名前です。学籍番号の最後の桁にパリティーチェック用の数字を加えたりしても名前だからOKです。
例:暗証番号
これも番号と言いながら、値の大小には意味がありません。順番とは無関係です。暗証番号は1つ違えば認証されません。
漢数字では大きな数は4桁ごとに名前が付けられている。SI単位系では3桁ごとに接頭語が用意されています。10進数でも大きな数になると桁が多すぎて読みにくくなります。
| 10進数 | 大きさ | 漢数字 | SI接頭辞 |
| 1 | 100 | 一 | |
| 10 | 101 | 十 | da:deca |
| 100 | 102 | 百 | h:hecto |
| 1000 | 103 | 千 | k:kiro |
| 10000 | 104 | 万 | |
| .... | |||
| 1000000 | 106 | (百万) | M:mega |
| .... | |||
| 100000000 | 108 | 億 | |
| 1000000000 | 109 | (十億) | G:giga |
| .... | |||
| 1000000000000 | 1012 | 兆 | T:tera |
| .... | |||
| 1000000000000000 | 1015 | (千兆) | P:peta |
| 10000000000000000 | 1016 | 京 | |
| .... |
1秒間に1回の浮動小数点演算を行う計算速度を 1 FLOPS(Floating-point Operations Per Second:フロップス)と言います。
最初の実用的計算機ENIACは300FLOPSと遅かった。0.3kFLOPS(キロ・フロップス)です。そして、スーパーコンピュータ「京」は1秒間に1京回の浮動小数点演算を行えるので、計算速度は10PFLOPS(ペタ・フロップス)となります。ENIACの30兆倍以上の計算能力です。
※1回の計算にかかる時間は、実はそこまで早くなっていません。スーパーコンピュータは演算回路を多数(10万個ほど)用意して同時に計算させることで計算量を増やしています。
30年前、計算機の計算速度は、1秒の間に100万回の浮動小数点演算ができるMFLOPS(メガ・フロップス)単位で話されていました。しかし、今ではこの言葉は聞くことが無くなりました。今のパソコンは1秒間に数十億回の計算ができるのでGFLOPS(ギガ・フロップス)単位の計算性能を持つからです。スパーコンピュータの場合は少し前までTFLOPS(テラ・フロップス)単位で計算能力が示されていましたが、今ではPFLOPS(ペタ・フロップス)単位になっています。
足し算の逆演算、引き算が常に可能なように数を拡張すると、整数になります。自然数にゼロと負の数が加わり、下限もなくなります。
数を大小の順番に並べるとマイナス無限大からプラス無限大まで1直線に並べることが可能です。従って、一つの直線上に等間隔で打たれた点を整数と1対1に対応させることができます。
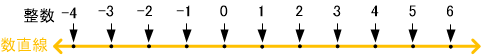
ここでの直線を数直線と呼ぶことにします。
さらに、掛け算の逆演算(除算)についても、0での除算を除いて閉じた数の集合に拡張したのが有理数です。
分数の形で表せる数として小学生のころから使ってきたと思います。
有理数をつかえば数直線上のすべての点と1対1の対応付けができるでしょうか?数直線上に0に対応する1点を定め、その点の左右にある点との距離を有理数で表し1対1の対応付けができるでしょうか?
有理数と数直線上の点の1対1の対応付けはできません。なぜなら、0点からの距離が無理数になる点、例えば円周率に等しい距離の点と対応する有理数は無いからです。
※有理数に対応する数直線上の点は無理数で無限に細かく切れています。値が連続ではないのです。
※円周率などの無理数と呼ばれる数に、幾らでも近い有理数が存在しますが、同じ値となる有理数は存在しません。
数直線上の全ての点に対応付け可能な連続した値を取る数。円周率πや√2のような無理数を含んだ集合です。
実数は長さなどの連続な量を表すのに適した数です。
従って、物理量(長さ、時間、電圧、電流、、、)の多くは実数値です。
※電子の個数とか例外的に整数値となるものもあります。
小中学校の教育では円周率を3とか3.14とか教えていても、円周率は3でや3.14に等しいわけではありません。正確に表現しようとすれば、πのように固有の名前を付けて表すしかありません。
しかし下記の円周率を少数で表記した例のように、小数を用いて実数に幾らでも近い数を書くことができます。有効数字の桁を増やすことで実数の値に近づくことは、どこまでも可能です。
円周率π〜
3
3.14
3.14159
3.1415926536
3.141592653589793
3.14159265358979323846
3.1415926535897932384626434
3.141592653589793238462643383279....
円周率の数字だけを乗せた本「円周率1000000桁表」も出版されている。現在では数十兆桁まで計算されているそうです。
少数は実数を近似的に表記する概数として使われます。10進少数は小数点と位取りの手法を用いて、1/10の桁、1/100の桁と細かい値の桁を表記することで実数に近い値を表現できます。桁数を増やすことで、どこまでも実数に近づけます。
※おおよその数を概数(がいすう)といいます。実数である円周率の代わりに使われる3とか3.14とかは概数です。概数については後述します。
しかし、実数値に等しい数を少数で示すことは通常はできません。地球の半径を実数R[km]とし、その値は6.371×103kmと表記しても、実際はR〜6.371×103でしかありません。ランダムに実数を取り出したとき、その値が有限桁の少数に等しくなる確率は1/∞と言っていいでしょう。
実数値は長さL、幅はWのように名前を付けて扱います。少数を用いて実数を表現する場合も、このあたりの数とか、この範囲の中にある数としか言えないのが通常です。
少数を用いて、L=3.14と表す場合はLは少数点以下3桁目で四捨五入すると3.14になる範囲の実数値という意味。あるいは、少し範囲を広げて3.13〜3.15の範囲の実数値といった意味になります。
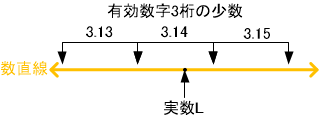
※測定値の場合は測定誤差があるので、さらに曖昧です。たとえば、Lが四捨五入すると3.14と表せる範囲にある確率は50%とといった表現が必要になります。
少数は実数の近似値を表しているので、どこまで近い値かが大事です。一番下の桁は多少の誤差を含んだ不確かな値となるようにした場合の桁数が有効数字です。
実数の値を少数で示す場合、ほとんどすべての場合に概数です。従って、大よその範囲がわかるように有効数字の桁数が明確にわかる書き方をすべきです。
例:
光の速さ30万km/sよりは3.0×105km/sのほうが明快。
30万km/sでは有効桁数が1桁なのか2桁なのかあいまいです。
3.0×105km/sなら有効桁数が2桁なのが明確です。
小さな数も、どれだけ小さいのかが大事です。SI単位系では3桁ごとに接頭語が用意されています。10進少数でも小さな数になると桁が多すぎて読みにくくなります。(漢字のほうは使うことが少ないので省きます)
| 10進数 | 大きさ | SI接頭辞 |
| 1 | 100 | |
| 0.1 | 10-1 | d:deci |
| 0.01 | 10-2 | c::centi |
| 0.001 | 10-3 | m:milli |
| .... | ||
| 0.000001 | 10-6 | μ:micro |
| .... | ||
| 0.000000001 | 10-9 | n:nano |
| .... | ||
| 0.000000000001 | 10-12 | p:pico |
| .... | ||
| 0.000000000000001 | 10-15 | f:femto |
| .... |
1mの千分の1が1mmです。細菌の大きさは数μmで可視光の波長は約800〜400nm。細菌は顕微鏡で何とか見えますが、ウイルスの大きさは300nm程度なので見えません。原子の大きさは1Å=0.1nm=100pm程度です。原子核の大きさは1fm。原子に比べて原子核の大きさは10万分の1です。
計算機が扱う数の基本は固定桁数の2進整数と2進少数です。
整数を固定桁数(8,16,32,64桁など)の2進整数として扱います。このため、整数と言いながら有限の下限と上限があり、計算結果がその範囲を超えた場合の扱いは色々です。
整数値は上限と下限の間であれば誤差のない計算ができます。
※ 整数の割り算は商と余りになるので有理数にはなりません。
計算機は実数を実数に一番近い固定桁数の2進少数として扱います。この結果、無理数だけでなく循環小数になる値も正確には扱えません。10進少数の0.1は2進少数では循環小数となるので、1.0+0.1+0.1の計算結果が1.2に等しくないといったことが起こります。(丸め誤差)
※ IEEE754の規格では
倍精度浮動小数点数(Cのdouble型で床われることが多い)は 少数点以下52桁、指数部11桁、符号1桁の0/1の64文字で扱う
計算機は実数を固定長の2進少数で近似して扱う。このため有効数字を表現できない。
計算させると沢山の桁を書き出します。有効数字が何桁かは人間が判断するしかありません。
例えば有効数字3桁の3.14は16桁固定長の10進少数では
3.140000000000000
となってしまい有効数字3桁という情報は扱えません。
10進少数で循環小数となる1/3は
0.333333333333333
となってしまい1/3に等しくはなりません
※有効数字のある値の四則演算は、それ用のプログラムを組むか、結果の有効数字を人間が判断する必要があります。
概数は大よその数です。何を概数とするかは目的に必要な精度によって変わります。
概数の例
| 数の名前 | 概数の値 |
| 日本の総人口 | 1億人 1億3000万人 12693万人 |
| 円周率 π | 3 3.14 3.1416 |
| √2 | 1.4 1.414 |
| ネイピア数 e | 2.7 2.718 |
| 地球の半径 | 6000km 6.371×103km |
| 光の速さ | 3×108m/s 2.998×108m/s |
実数の概数を有効数字を使った少数とすることが多い。たとえば、円周率の概数として3.14がよく使われます。
概数の幅の割合が小さいことを前提にして、四則演算での有効数字の見積もりかたは決めています。
有効数字が1桁もないような数値は有効数字を用いて表現するのは困難です。そんな計算でも値のオーダーを知りたい場合があります。
※オーダー(order) ここでは、物理学的用語として10、100、1000、、、のような桁の意味で使う。
1961年「我々の銀河系に存在し人類とコンタクトする可能性のある地球外文明の数」としてフランク・ドレイクが提唱した式
N=R*×f p ×ne ×fl ×fi
×fe ×L
=10× 0.5 ×2
×1 ×0.01×0.01×10000
=10 <<この値は2桁以上違うかも知れません。
変数の意味
R*[個/年] (銀河系の生涯を通じて、年平均10個の恒星が誕生する)
fp(あらゆる恒星のうち半数が惑星を持つ)
ne(惑星を持つ恒星は、生命が誕生可能な惑星を二つ持つ)
fl(生命が誕生可能な惑星では、100%生命が誕生する)
fi(生命が誕生した惑星の1%で知的文明が獲得される)
fe(知的文明を有する惑星の1%が通信可能となる)
L[年] (通信可能な文明は1万年間存続する)
全ての数値が有効数字1桁もない概数です。仮に全て半分にしたら128分の1に、倍にしたら128倍になる。
測定値には必ず誤差が含まれます。そこで測定値の何桁目まで信用できるか,あるいは意味があるかを示すために、少数を用い、有効数字で不確かさの程度を示します。有効数字は曖昧な部分もありますが、誤差範囲を示す簡便な方法としてよく使われます。
1.00cmと書けば四捨五入して1.00になる。つまり最小でも±0.005cm程度は値に誤差があることを示しています。
有効数字を持つ値の加算結果は、誤差(不確かさの幅)が最大の値に合わせて有効数字が決まる。独立した誤差を含む値をたくさん足したり引いたりしても誤差は増えることはあっても、減りはしません。
● 幅1.02cmで長さが10.00mの細長い長方形の周囲の長さは?
2×( 10.00m +
0.0102m ) = 20.02m ※2×の2は整数なので誤差はありません
● 重さ1.0×104kg(=10トン)のトラックに体重163kgの相撲取りが乗ったら、合わせた重量は?
1.0×104kg + 1.63×102kg
= 1.0×104kg ※重量は増えますが、増加分はトラック重量の誤差範囲内で少数値に現れない。
● トラックに体重163kgの相撲取りが10人乗ったら、合わせた重量は?^^
上の計算で一人づつ足していったらいつまでたっても10トンのままでしょうか?そんなことはないはずです。
1.0×104kg + 10×(1.63×102kg)
= 1.0×104kg + 163×10kg = 1.2×104kg ※四捨五入したので数値は2トン増えた
計算機で加減算するときは、出力された少数から、入力値の中で一番誤差の大きな値に合わせて、有効数字の範囲だけを計算結果としてください。計算機は有効数字を考えてくれないので人間が決めなくてはいけません。
有効数字を持つ値の積算結果は、誤差の割合が最大の値に合わせて有効数字が決まる。独立した誤差を含む値をたくさん掛けたり割ったりしても、誤差の割合は増えることはあっても、減りはしません。
● 幅1.02cmで長さが10.00mの細長い長方形の面積は?
10.00m ×
0.0102m = 0.102m2 ※有効数字は3桁
●半径1.2cmの円の面積は?
3.14×(1.2cm)2=4.5cm2
●半径1.234mの円の面積は?
3.1416×(1.234m)2=4.784m2 ※円周率は3.14では正確さが足りません半径の有効数字より1桁多くして使いました
計算機で掛け算や割り算をするとき、入力値の中で一番有効数字の桁が少ない値(誤差割合の大きな値)に合わせて、有効数字の範囲だけを計算結果としてください。円周率πや自然対数の底eなどが含まれるときは、入力の有効桁数よりも大きな有効桁数を入力すること。
非常に大きな数や小さな数を掛けたり割ったりする場合は、値の大きさに注意。
電卓を使って計算しても桁を間違えることは多い^^。
値A,Bの誤差をa,bとしましょう
(A±a)×(B±b)= AB±aB±Ab±ab
=AB{ 1±a/A±b/B±ab/AB }
ここで誤差の割合が 1 >> a/A >> b/B であれば 計算結果の誤差は約 a/A です。もしもa/A =b/B なら誤差は大きくても約 2a/A です。2倍程度は無視することにします。有効数字の少ない(誤差の割合が大きい)ほうに合わせて計算結果の有効数字を決めるのは、このような理由です。
※a/A や b/B は1よりも十分い小さいことを仮定しました、これが成立しないときは、有効数字の計算ルールではうまくいきません。
細長い長方形の2辺がw=1.01cmとh=20.5cmであるときその周囲の長さL=2w+2hと面積S=w×hは幾らになりますか。有効数字に注意して解答して下さい。
一般に測定を行って得られた値には必ず誤差が含まれます。誤差には物差しの目盛りの不正などの系統的誤差や、何らかの過失などによる誤差などその大きさや原因が明らかなものもあります。これらは実験において十分注意して取り除かねばなりません。しかし、それでも何がしか、偶然に支配される誤差が残ります。これを偶然誤差と言います。
偶然誤差の性質を知るためには同じ条件で非常に多くの測定を行い。その測定値がどのように分布しているかを調べなければなりません。実際にそのような測定を行うと、多くの場合に正規分布と呼ばれる同じ形が得られます。
注意:そこで、今後は、正規分布に従う場合について話を進めていきます。正規分布で無い場合以下の話は成立しません 。
正規分布はガウス分布ともいわれ真値からの誤差が値xをとる確率密度p(x)は次のグラフの様な関数形をしています。ここで、 σは標準偏差と言われる値で関数の広がりの程度を示します。 図はσ=1の場合でxの正負で対象な釣り鐘の形をした関数です。
ある範囲内の値が観測される確率はその範囲で確率密度を積分した値になり、
誤差xが±σの範囲に入る確率は68%、±2σでは95%、±3σでは99.7%となります。
逆に確率が1/2になる範囲は±0.6745σ。
p(x)=exp(-x2/2σ2)/(σ√2p )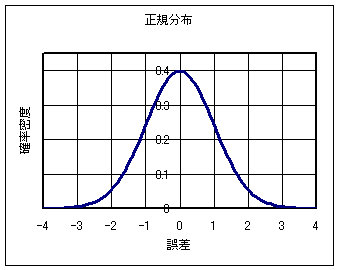
誤差分布まで調べるには無限個の測定が必要となる。しかし、実際の測定では有限個の値しか測定できない。ここで、無限回の測定をした場合の測定値集団を母集団と呼ぶことにし、実際のn回の測定で求めた値の集団を標本と呼ぶことにしよう。
母集団が正規分布に従うとき真値と標準偏差を決めればその分布は決まる。このような母集団の特性を決めるパラメータを母数と言います。ところで、問題は標本から真値と標準偏差をいかに推定するかです。以下に結論を述べます。
標本の平均(相加平均)はnが大きくなると真値に収束します。そこで、平均値を真値の推定値とし最確値と呼ぶことにします。ここで、標本を何度も取り直した場合、最確値は真値のまわりに標準偏差σm=σ/√nで分布する正規分布を示します。つまり、最確値はn個のデータを平均した結果、1個の測定値に比べて バラつきの範囲が√n分の1に小さくなります。
標準偏差σは母集団の分散(誤差の2乗平均)の平方根に等しいが、標本でも各測定値Miと最確値Xmの差(これを残差と言う)の2乗平均Σ(Mi−Xm)2/nが分散の目安になりそうです。しかし、n=1の場合を考えてみると測定値がそのまま最確値となり分散の推定値は0になってしまいます。これは変です。実は分散の推定値はΣ(Mi−Xm)2/(n−1)になります。ここで−1するのは最確値を求めたので標本のデータを1個分使ってしまい残りのn−1個分から分散を推定するためです。
標準偏差の推定値=√{Σ(Mi−Xm)2/(n−1)}
最確値Xmの標準偏差はσm=σ/√n=√{Σ(Mi−Xm)2/n(n−1)}
※試験の成績のように母集団の全てが分かっているときは、その集団の平均値Xm=(ΣMi)/n、標準偏差=√{Σ(Mi−Xm)2/n} と計算されます。n=1の場合、母集団の値は1個ですから当然ながら、バラツキはありません。上記は母集団の一部分しか分からない状況で推定値を計算していることに注意してください。
最確値を誤差範囲まで合わせて示す10.02±0.41のような表記法がよく使われる。ここで示される値は確率が1/2の誤差範囲を用いたXm±0.6745σmあるいは標準偏差をそのまま用いたXm±σmである。
注:nが十分に大きい場合には確率1/2の誤差範囲は±0.6745σmに収束するが、nが小さい場合は、n=2では±σm、n=3では±0.82σm、n=4では±0.77σmと範囲が広い。以下に90%や99%の範囲も合わせて表を示す。ここで、例えば測定3回の平均値が真値から±2.92σm以上異なるなる確率は10%であることがわかる。
| 測定回数 | 50%の範囲 | 90%の範囲 | 99%の範囲 |
| 2 | ±1.00σm | ±6.31σm | ±63.66σm |
| 3 | ±0.82σm | ±2.92σm | ±9.93σm |
| 4 | ±0.77σm | ±2.35σm | ±5.84σm |
| 10 | ±0.70σm | ±1.83σm | ±3.25σm |
| ∞ | ±0.67σm | ±1.65σm | ±2.58σm |
表のデータを確認するためのプログラムを作りました。真値と標準偏差からガウス分布する乱数を使って測定値を作ります。標本数のデータを測定し、最確値と最確値の標準偏差を求めます。
測定値M±mの演算結果の誤差について結論を以下に示す。これらの結論は正規分布を仮定して求められた結果である。
定数a倍 a×M −−>aM±am
和 M1+M2 −−>M1+M2± √(m12+m22)
一般の場合(誤差は微小と仮定しテーラー展開の1次の項までを考慮する)
f(M1、M2)−−> f(M1、M2)± √{(df/dM1)2m12+(df/dM2)2m22}
一般の場合に積をあてはめると M1×M2 −−>M1×M2± √(M22m12+M12m22)
有効数字の計算規則と、上記の結論とがどの程度異なるかを問題2-1を例として示しなさい。
w=1.010±0.005 cm
h=20.50±0.05cm あるいは w=1.01±0.01 cm h=20.5±0.1cm として計算すること
同じ量についての異なる複数の測定値からもっとも確からしい値(最確値)をどのように求めれば良いのか?その一つの解答として最小2乗法がよく知られています。
未知の値Xmと測定値Miの差をri=Mi−Xmとしたとき、riの2乗和S=Σ(Mi−Xm)2 を最小にするXmを求めよう。 SをXmの関数と見れば、dS/dXm=0になるときSは極小となる。
dS/dXm=-Σ2(Mi−Xm)
これが0になる条件からnXm=ΣMiつまりXmが相加平均ΣMi/nのときに2乗和Sは最小値となることが示される
これまで用いてきた最確値はこの最小2乗法から見た最適値でもある
最適値と言うときには何を基準に選択したかが重要です。 最小二乗法の他にも、最適な何かを求める手法として最大エントロピー法などもあります。
実際に簡単な測定を行って、最確値や標準偏差を見積もり、誤差表記のある結果を求めてみましょう。
配布したプリントの長方形の縦と横の長さを測ってもらいますが、ちょっと変わった測り方をしますので、説明をよく聞いてから始めてください。平方根などは計算機が目の前にあるのできちんと計算してください。計算機は小数点以下何桁でも書き出しますが、皆さんは有効数字を判断して結果をレポートに書いてください。
レポートを書くときは レポートの注意点を参考にしてください。
以下の長方形について縦と横の2辺の長さを各10回測定し長方形の面積を求めなさい。途中の計算も含めて示すこと。計測は長方形の外枠を測定すること。誤差範囲は50%の範囲を示して下さい。
|
|
辺の長さの測定では物差しの原点を辺の端に合わせて長さを読んではいけない。物差しを辺に重ね両端の値を其々0.1mmまでよみ記録する。その差から長さを求めよ。また測定の度に物差しをずらして測ること。これは、目盛りを読むときの人間の癖(系統的誤差の一つ)が影響するのを避けるためでもある。
※エクセルで表を作っても構いませんが、その場合は値の表示桁数に注意してください。エクセルは有効数字を教えてはくれないので自分で考えよう。
| No. | 右端[mm] | 左端[mm] | 長さMi[mm] | 残差ri[mm] | 残差2[mm2] |
| 1 |
|
|
|
| |
| 2 |
|
|
| ||
| 3 |
|
|
| ||
| 4 |
|
|
| ||
| 5 |
|
|
| ||
| 6 |
|
|
| ||
| 7 |
|
|
| ||
| 8 |
|
|
| ||
| 9 |
|
|
| ||
| 10 |
|
|
| ||
| 合計 | −−−−− | −−−−− | −−−−− |
最確値Xm=ΣMi/n
※最確値は測定値と同じ有効数字にはなりません。平均しているので誤差が減っています。√10分の1になるので、1桁増やしておきましょう。
母集団 標準偏差 の推定値σ=√{Σri2/(n−1)}
最確値の標準偏差σm=σ/√n
横の辺の長さ= ± [mm]
※計算は有効数字を考えずに計算機で計算し、最後に結果をレポートに書くところで有効数字を入れましょう。
横と同様に縦の辺の長さや誤差範囲を50%の範囲で求めなさい
| No. | 上端[mm] | 下端[mm] | 長さ[mm] | 残差[mm] | 残差2[mm2] |
| 1 |
|
|
|
|
|
| 2 |
|
|
|
|
|
| 3 |
|
|
|
|
|
| 4 |
|
|
|
|
|
| 5 |
|
|
|
|
|
| 6 |
|
|
|
|
|
| 7 |
|
|
|
|
|
| 8 |
|
|
|
|
|
| 9 |
|
|
|
|
|
| 10 |
|
|
|
|
|
| 合計 | −−−−− | −−−−− |
| −−−−− |
|
誤差の伝搬を思い出して、面積の最確値と誤差範囲を計算しなさい。